期望值

在概率和统计学中，期望或期望值是随机变量的加权平均值。

连续随机变量的期望

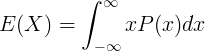
E(X)=\int_{-\infty }^{\infty }xP(x)dx

E(X) 是连续随机变量 X 的期望值

x 是连续随机变量 X 的值

P(x) 是概率密度函数

离散随机变量的期望

E(X)=\sum_{i}^{}x_iP(x)

E(X) 是连续随机变量 X 的期望值

x 是连续随机变量 X 的值

P(x) 是 X 的概率质量函数

期望的性质

线性性

当 a 是常数，X,Y 是随机变量时：

E(aX) = aE(X)

E(X+Y) = E(X) + E(Y)

常数

当 c 是常数时：

E(c) = c

乘积

当 X 和 Y 是独立随机变量时：

E(X ⋅Y) = E(X) ⋅ E(Y)

条件期望


另见

可否帮我们改进此页面

概率与统计
站点内容