e常数

e常数或欧拉数是一个数学常数。e常数是实数且是无理数。

e = 2.718281828459...

e的定义
e的性质
以e为底的对数
指数函数
欧拉公式

e的定义

e常数定义为极限：

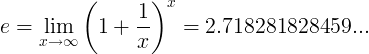
$e=\lim_{x\rightarrow \infty }\left ( 1+\frac{1}{x} \right )^x = 2.718281828459...$

其他定义

e常数定义为极限：

$e=\lim_{x\rightarrow 0 }\left ( 1+ \right x)^\frac{1}{x}$

e常数定义为无穷级数：

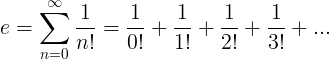
$e=\sum_{n=0}^{\infty }\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+...$

e的性质

e的倒数

e的倒数是极限：

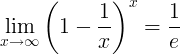
$\lim_{x\rightarrow \infty }\left ( 1-\frac{1}{x} \right )^x=\frac{1}{e}$

e的导数

指数函数的导数是指数函数本身：

(e^x)' = e^x

自然对数函数的导数是倒数函数：

(log_ex)' = (ln x)' = 1/x

e的积分

指数函数e^x的不定积分是指数函数e^x。

∫ e^xdx = e^x+c

自然对数函数log_ex的不定积分是：

∫ log_ex dx = ∫ lnx dx = x ln x - x +c

倒数函数1/x从1到e的定积分是1：

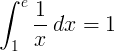
$\int_{1}^{e}\frac{1}{x}\: dx=1$

以e为底的对数

数字x的自然对数定义为以e为底的x的对数：

ln x = log_ex

指数函数

指数函数定义为：

f (x) = exp(x) = e^x

欧拉公式

复数e^iθ具有恒等式：

e^iθ = cos(θ) + i sin(θ)

i是虚数单位（-1的平方根）。

θ是任意实数。

e常数