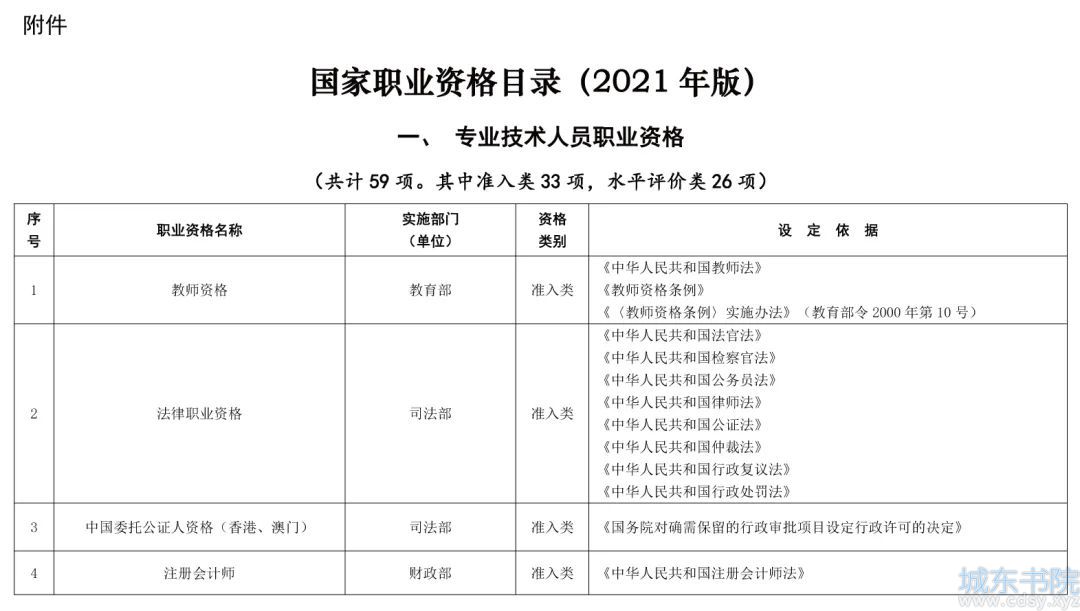
矩阵求导术

矩阵求导的技术，在统计学、控制论、机器学习等领域有广泛的应用。鉴于我看过的一些资料或言之不详、或繁乱无绪，本文来做个科普，分作两篇，上篇讲标量对矩阵的求导术，下篇讲矩阵对矩阵的求导术。本文使用小写字母x表示标量，粗体小写字母  表示（列）向量，大写字母X表示矩阵。

首先来琢磨一下定义，标量f对矩阵X的导数，即f对X逐元素求导排成与X尺寸相同的矩阵。然而，这个定义在计算中并不好用，实用上的原因是在对较复杂的函数难以逐元素求导；哲理上的原因是逐元素求导破坏了整体性。试想，为何要将f看做矩阵X而不是各元素  的函数呢？答案是用矩阵运算更整洁。所以在求导时不宜拆开矩阵，而是要找一个从整体出发的算法。

为此，我们来回顾，一元微积分中的导数（标量对标量的导数）与微分有联系；多元微积分中的梯度（标量对向量的导数）也与微分有联系：  ，这里第一个等号是全微分公式，第二个等号表达了梯度与微分的联系：全微分  是  梯度向量  与  微分向量  的内积；受此启发，我们将矩阵导数与微分建立联系：  。其中tr代表迹(trace)是方阵对角线元素之和，满足性质：对尺寸相同的矩阵A,B，即 是矩阵A,B的内积。与梯度相似，这里第一个等号是全微分公式，第二个等号表达了矩阵导数与微分的联系：全微分  是  导数  与  微分矩阵  的内积。

然后来建立运算法则。回想遇到较复杂的一元函数如  ，我们是如何求导的呢？通常不是从定义开始求极限，而是先建立了初等函数求导和四则运算、复合等法则，再来运用这些法则。故而，我们来创立常用的矩阵微分的运算法则：

1. 加减法：  ；矩阵乘法：  ；转置：  ；迹：  。
2. 逆：  。此式可在两侧求微分来证明。
3. 行列式：  ，其中  表示X的伴随矩阵，在X可逆时又可以写作  。此式可用Laplace展开来证明，详见张贤达《矩阵分析与应用》第279页。
4. 逐元素乘法：  ，  表示尺寸相同的矩阵X,Y逐元素相乘。
5. 逐元素函数：  ，  是逐元素标量函数运算，  是逐元素求导数。举个例子，  。

我们试图利用矩阵导数与微分的联系，在求出左侧的微分 后，该如何写成右侧的形式并得到导数呢？这需要一些迹技巧(trace trick)：

1. 标量套上迹： 
2. 转置：  。
3. 线性：  。
4. 矩阵乘法交换：  ，其中  与  尺寸相同。两侧都等于  。
5. 矩阵乘法/逐元素乘法交换：  ，其中  尺寸相同。两侧都等于  。

观察一下可以断言，若标量函数f是矩阵X经加减乘法、行列式、逆、逐元素函数等运算构成，则使用相应的运算法则对f求微分，再使用迹技巧给df套上迹并将其它项交换至dX左侧，即能得到导数。

在建立法则的最后，来谈一谈复合：假设已求得  ，而Y是X的函数，如何求  呢？在微积分中有标量求导的链式法则  ，但这里我们不能沿用链式法则，因为矩阵对矩阵的导数  截至目前仍是未定义的。于是我们继续追本溯源，链式法则是从何而来？源头仍然是微分。我们直接从微分入手建立复合法则：先写出  ，再将dY用dX表示出来代入，并使用迹技巧将其他项交换至dX左侧，即可得到  。

接下来演示一些算例。特别提醒要依据已经建立的运算法则来计算，不能随意套用微积分中标量导数的结论，比如认为AX对X的导数为A，这是没有根据、意义不明的。

例1： 求  。其中  是  列向量，  是  矩阵，  是  列向量，  是标量。

解：先使用矩阵乘法法则求微分，这里的  是常量，  ，得到：  ，再套上迹并做矩阵乘法交换：  ，注意这里我们根据  交换了与  。对照导数与微分的联系  ，得到  。

注意：这里不能用  ，导数与乘常数矩阵的交换是不合法则的运算（而微分是合法的）。有些资料在计算矩阵导数时，会略过求微分这一步，这是逻辑上解释不通的。

例2：  ，求 。其中  是  列向量，  是  矩阵，  是  列向量，exp表示逐元素求指数， 是标量。

解：先使用矩阵乘法、逐元素函数法则求微分：  ，再套上迹并做矩阵乘法/逐元素乘法交换、矩阵乘法交换：  ，注意这里我们先根据  交换了 、  与  ，再根据  交换了  与  。对照导数与微分的联系 ，得到  。

例3【线性回归】：  ， 求  的最小二乘估计，即求  的零点。其中  是  列向量， 是  矩阵，  是  列向量，  是标量。

解：严格来说这是标量对向量的导数，不过可以把向量看做矩阵的特例。先将向量模平方改写成向量与自身的内积：  ，求微分，使用矩阵乘法、转置等法则：  。对照导数与微分的联系  ，得到  。  的零点即  的最小二乘估计为  。

例4【方差的最大似然估计】：样本  ，求方差  的最大似然估计。写成数学式是：  ，求  的零点。其中  是  列向量，  是样本均值，  是  对称正定矩阵，  是标量。

解：首先求微分，使用矩阵乘法、行列式、逆等运算法则，第一项是  ，第二项是  。再给第二项套上迹做交换：    ，其中先交换迹与求和，然后将 交换到左边，最后再交换迹与求和，并定义  为样本方差矩阵。得到  。对照导数与微分的联系，有  ，其零点即  的最大似然估计为  。

例5【多元logistic回归】： 求  。其中  是除一个元素为1外其它元素为0的  列向量，  是  矩阵，  是  列向量，  是标量；  ，其中  表示逐元素求指数，  代表全1向量。

解：首先将softmax函数代入并写成  ，这里要注意逐元素log满足等式  ，以及  满足  。求微分，使用矩阵乘法、逐元素函数等法则：  。再套上迹并做交换，注意可化简  ，这是根据等式  ，故  。对照导数与微分的联系，得到  。

另解：定义  ，则  ，先如上求出  ，再利用复合法则：  ，得到  。

最后一例留给经典的神经网络。神经网络的求导术是学术史上的重要成果，还有个专门的名字叫做BP算法，我相信如今很多人在初次推导BP算法时也会颇费一番脑筋，事实上使用矩阵求导术来推导并不复杂。为简化起见，我们推导二层神经网络的BP算法。

例6【二层神经网络】：  ，求  和  。其中  是除一个元素为1外其它元素为0的的  列向量，  是  矩阵，  是  矩阵，  是  列向量， 是标量；  同例3，  是逐元素sigmoid函数  。

解：定义  ，  ，  ，则  。在前例中已求出  。使用复合法则，注意此处  都是变量：  ，使用矩阵乘法交换的迹技巧从第一项得到  ，从第二项得到  。接下来求  ，继续使用复合法则，并利用矩阵乘法和逐元素乘法交换的迹技巧：  ，得到  。为求  ，再用一次复合法则：  ，得到  。

使用小写字母x表示标量，粗体小写字母  表示列向量，大写字母X表示矩阵。矩阵对矩阵的求导采用了向量化的思路，常应用于二阶方法求解优化问题。

首先来琢磨一下定义。矩阵对矩阵的导数，需要什么样的定义？第一，矩阵F(p×q)对矩阵X(m×n)的导数应包含所有mnpq个偏导数  ，从而不损失信息；第二，导数与微分有简明的联系，因为在计算导数和应用中需要这个联系；第三，导数有简明的从整体出发的算法。我们先定义向量  (p×1)对向量  (m×1)的导数  (m×p)，有  ；再定义矩阵的（按列优先）向量化  (mn×1)，并定义矩阵F对矩阵X的导数 (mn×pq)。导数与微分有联系  。几点说明如下：

1. 按此定义，标量f对矩阵X(m×n)的导数  是mn×1向量，与上篇的定义不兼容，不过二者容易相互转换。为避免混淆，用记号  表示上篇定义的m×n矩阵，则有  。虽然本篇的技术可以用于标量对矩阵求导这种特殊情况，但使用上篇中的技术更方便。读者可以通过上篇中的算例试验两种方法的等价转换。
2. 标量对矩阵的二阶导数，又称Hessian矩阵，定义为  (mn×mn)，是对称矩阵。对向量  或矩阵  求导都可以得到Hessian矩阵，但从矩阵  出发更方便。
3. 求导时矩阵被向量化，弊端是这在一定程度破坏了矩阵的结构，会导致结果变得形式复杂；好处是多元微积分中关于梯度、Hessian矩阵的结论可以沿用过来，只需将矩阵向量化。例如优化问题中，牛顿法的更新  ，满足  。
4. 在资料中，矩阵对矩阵的导数还有其它定义，比如 (mp×nq)，它能兼容上篇中的标量对矩阵导数的定义，但微分与导数的联系（dF等于  中每个m×n子块分别与dX做内积）不够简明，不便于计算和应用。

然后来建立运算法则。仍然要利用导数与微分的联系  ，求微分的方法与上篇相同，而从微分得到导数需要一些向量化的技巧：

1. 线性：  。
2. 矩阵乘法：  ，其中  表示Kronecker积，A(m×n)与B(p×q)的Kronecker积是  (mp×nq)。此式证明见张贤达《矩阵分析与应用》第107-108页。
3. 转置：  ，A是m×n矩阵，其中  (mn×mn)是交换矩阵(commutation matrix)。
4. 逐元素乘法：  ，其中  (mn×mn)是用A的元素（按列优先）排成的对角阵。

观察一下可以断言，若矩阵函数F是矩阵X经加减乘法、行列式、逆、逐元素函数等运算构成，则使用相应的运算法则对F求微分，再做向量化并使用技巧将其它项交换至vec(dX)左侧，即能得到导数。

再谈一谈复合：假设已求得  ，而Y是X的函数，如何求 呢？从导数与微分的联系入手，  ，可以推出链式法则  。

和标量对矩阵的导数相比，矩阵对矩阵的导数形式更加复杂，从不同角度出发常会得到形式不同的结果。有一些Kronecker积和交换矩阵相关的恒等式，可用来做等价变形：

1.  。
2.  。
3.  。可以对  求导来证明，一方面，直接求导得到  ；另一方面，引入  ，有  ，用链式法则得到  。
4.  。
5.  ，A是m×n矩阵，B是p×q矩阵。可以对  做向量化来证明，一方面，  ；另一方面，  。

接下来演示一些算例。

例1：  ，X是m×n矩阵，求 。

解：先求微分：  ，再做向量化，使用矩阵乘法的技巧，注意在dX右侧添加单位阵：  ，对照导数与微分的联系得到  。

特例：如果X退化为向量，即  ，则根据向量的导数与微分的关系  ，得到  。

例2：  ，X是n×n矩阵，求  和  。

解：使用上篇中的技术可求得  。为求  ，先求微分：  ，再做向量化，使用转置和矩阵乘法的技巧  ，对照导数与微分的联系，得到  ，注意它是对称矩阵。在  是对称矩阵时，可简化为  。

例3：  ，A是l×m矩阵，X是m×n矩阵，B是n×p矩阵，exp为逐元素函数，求 。

解：先求微分：  ，再做向量化，使用矩阵乘法的技巧：  ，再用逐元素乘法的技巧：  ，再用矩阵乘法的技巧：  ，对照导数与微分的联系得到  。

例4【一元logistic回归】： 求  和  。其中  是取值0或1的标量，  是  列向量。

解：使用上篇中的技术可求得  ，其中  为sigmoid函数。为求  ，先求微分：  ，其中  为sigmoid函数的导数，对照导数与微分的联系，得到  。

推广：样本  ，  ，求  和  。有两种方法，方法一：先对每个样本求导，然后相加；方法二：定义矩阵  ，向量  ，将  写成矩阵形式  ，进而可以求得  ，  。

例5【多元logistic回归】：  ，求  和  。其中其中  是除一个元素为1外其它元素为0的  列向量，  是  矩阵，  是  列向量， 是标量。

解：上篇中已求得  。为求  ，先求微分：定义  ，  ，这里需要化简去掉逐元素乘法，第一项中  ，第二项中  ，故有  ，其中  ，代入有  ，做向量化并使用矩阵乘法的技巧，得到  。

最后做个总结。我们发展了从整体出发的矩阵求导的技术，导数与微分的联系是计算的枢纽，标量对矩阵的导数与微分的联系是  ，先对f求微分，再使用迹技巧可求得导数，特别地，标量对向量的导数与微分的联系是  ；矩阵对矩阵的导数与微分的联系是  ，先对F求微分，再使用向量化的技巧可求得导数，特别地，向量对向量的导数与微分的联系是  。

参考资料：

1. 张贤达.矩阵分析与应用. 清华大学出版社有限公司, 2004.
2. Fackler, Paul L. "Notes on matrix calculus."North Carolina State University(2005).
3. Petersen, Kaare Brandt, and Michael Syskind Pedersen. "The matrix cookbook."_Technical University of Denmark_7 (2008): 15.
4. HU, Pili. "Matrix Calculus: Derivation and Simple Application." (2012)