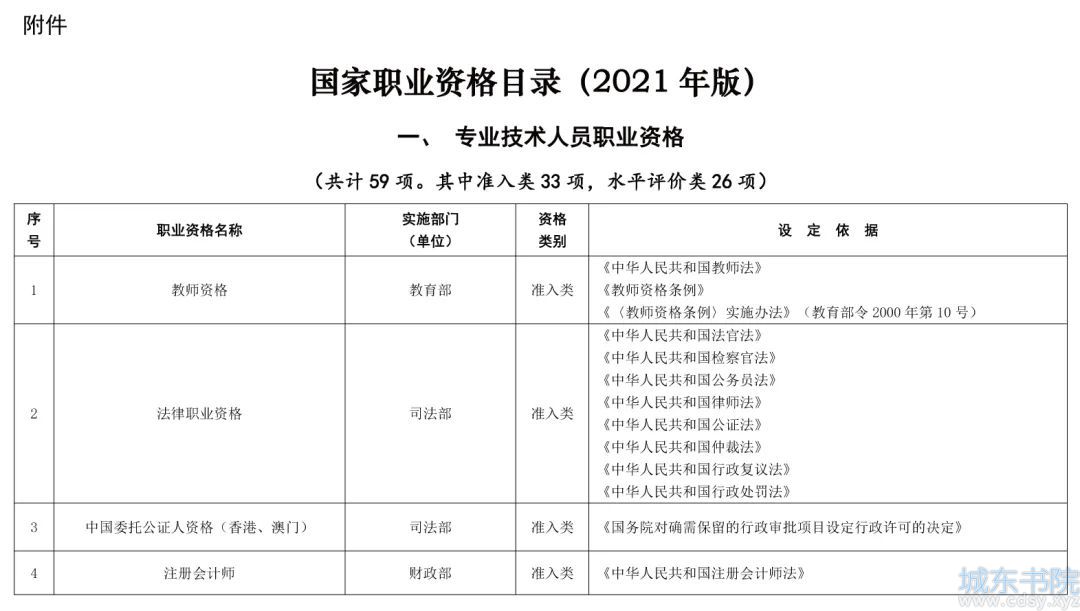
高斯狂想曲，非常强大的高斯积分（求解技巧）

高斯积分几乎出现在数学和物理的所有领域，甚至在你意想不到的地方。高斯函数和𝑁维中的球体的体积有密切关系。高斯积分很强大，我希望在阅读完这篇文章后，你会同意。

高斯积分是以伟大的德国数学家卡尔·弗里德里希的名字命名的

它描述了位于𝑥=𝜇附近的钟形曲线下的面积，下方绘制的宽度对应于𝜎

• 高斯积分是钟形高斯函数下的面积

我经常看到这个积分，但我总是记不住把这些常数放在哪里。前面的因数是2𝜋还是𝜋？𝜎是在平方根里面还是外面？指数是1还是1/2？

首先，让我们做一个最简单的高斯积分例子。

计算𝐼的诀窍是先计算𝐼²，然后取平方根。解出来后，就很容易计算

只需要做替换𝑥→𝑎𝑥，重复使用更简单的积分，

同样，我们得到

代换𝑥→𝑥−𝜇。只是稍微复杂一点的是

要做到这一点，只需计算

重新使用上面计算的积分：

同时，我们现在知道了高斯函数的傅里叶变换。只需替换前面结果中的𝑏→𝑖𝑏。几乎不经过计算，但经过论证，就得到了广义多维版本

𝐴是一些（正）对称𝑁×𝑁矩阵（不一定对角线）和𝑥是列向量

论证如下。由于𝐴是一个对称矩阵，我们可以找到一个正交矩阵O，其det O=1

其中𝐷是一个对角矩阵。然后我们有

现在我们的替代

所以

𝐽是替换变换的雅可比矩阵。但是这个替换的雅可比矩阵是𝑂正交矩阵的行列式是1。由于𝐷是一个对角矩阵，我们有

其中𝑑_𝑘𝑘是行𝑘和列𝑘𝐷的值。所以我们有

似乎我们将问题简化为从矩阵𝐴确定对角矩阵𝐷。但我们甚至不需要它。因为det𝑂=det O^T = 1

这就是广义的𝑁-维l例子的最终结果。可能有点复杂，但我认为这是一个很酷的计算。