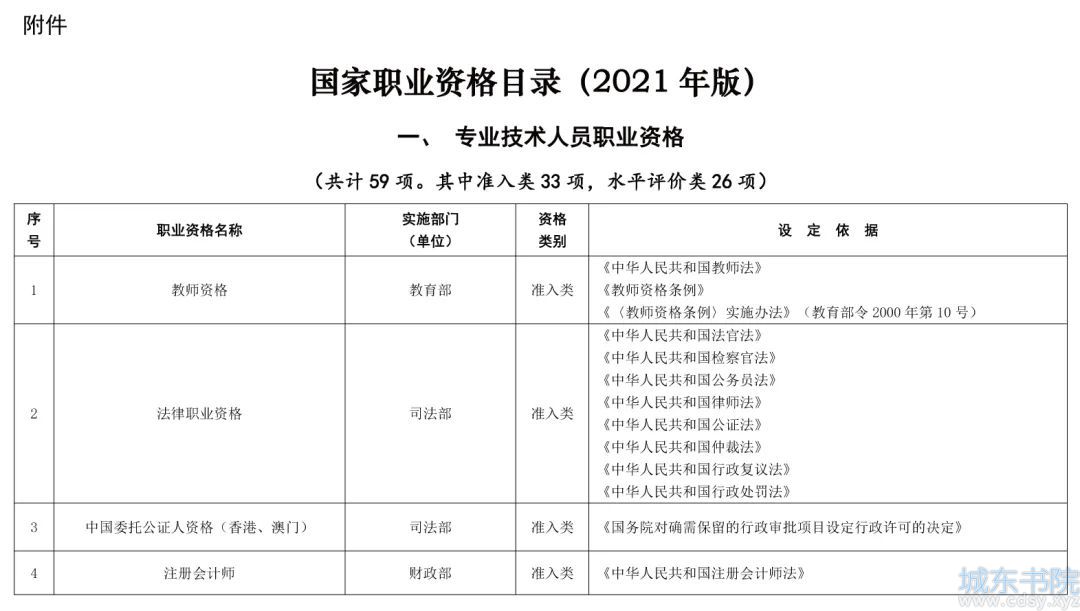
算法 排序算法
时间:12-14来源:作者:点击数:
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 希尔排序 | O(n1.3) | O(n2) | O(n) | O(1) | 不稳定 |
| 选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 |
| 冒泡排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 快速排序 | O(nlog2n) | O(n2) | O(nlog2n) | O(nlog2n) | 不稳定 |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 |
| 基数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
冒泡排序 O(n2)
思路:
- 从数组开始比较相邻的 2 个元素,前者比后者大的话,两者交换位置。
- 对每一对相邻元素做相同操作,从开始第一对到最后一对,把数值最大的元素排到最后面。
- 针对 n 个元素重复以上步骤,每次循环排除当前最后一个。
- 重复步骤 1~3,直到排序完成。
// 最外层循环控制的内容是循环次数
// 每一次比较的内容都是相邻两者之间的大小关系
let BubbleSort = function (arr, flag = 0) {
let len = arr.length - 1;
for (let i = 0; i < len; i++) { // 每次循环都得到剩余元素的最大值
for (let j = 0; j < len - i; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
}
}
}
return flag ? arr.reverse() : arr
}
let arr = [2, 9, 6, 7, 4, 3, 1, 7]
console.log(BubbleSort(arr, 1))
基数排序 O(n+k)
它的思想:就是把数组元素作为数组的下标,然后用一个临时数组统计该元素出现的次数。
数组的数据必须是整数,而且最大最小值相差的值不要过大,对于 数据是负数的话,我实现的方案对此有优化 。
思路
- 计算出差值 d,最小值小于 0,加上本身 add
- 创建统计数组并统计对应元素个数
- 统计数组做变形,后面的元素等于前面的元素之和,也就是排名数组
- 遍历原始数组,从统计数组中找到正确位置,输出到结果数组

// 计数排序
let countingSort = function(arr, flag = 0) {
let min = arr[0],
max = arr[0],
len = arr.length;
// 求最大最小值
for(let i = 0; i < len; i++) {
max = Math.max(arr[i], max)
min = Math.min(arr[i], min)
}
// 1.计算出差值 d,最小值小于 0,加上本身 add
let d = max - min,
add = min < 0 ? -min : 0;
//2.创建统计数组并统计对应元素个数
let countArray = new Array(d+1+add).fill(0)
for(let i = 0; i < len; i++){
let demp = arr[i]- min + add
countArray[ demp ] += 1
}
//3.统计数组做变形,后面的元素等于前面的元素之和,也就是排名数组
let sum = 0;
// 这里需要遍历的是 countArray 数组长度
for(let i = 0; i < d+1+add; i++){
sum += countArray[i]
countArray[i] = sum;
}
let res = new Array(len)
//4.遍历原始数组,从统计数组中找到正确位置,输出到结果数组
for(let i = 0; i < len; i++){
let demp = arr[i] -min + add
res[ countArray[demp] -1 ] = arr[i]
countArray[demp] --;
}
return flag ? res.reverse() : res
}
let arr = [2, 9, 6, 7, 4, 3, 1, 7,0,-1,-2]
console.log(countingSort(arr))
快速排序 O(n2)
通过一趟排序将待排数组分隔成独立的两部分,其中一个数组的元素均比另一数组的元素小,则可分别对这两部分数组继续进行排序,以达到整个数组有序
思路:
- 选择数组中间数作为基数,并从数组中取出此基数
- 准备两个数组容器,遍历数组,逐个与基数比对,较小的放左边容器,较大的放右边容器;
- 递归处理两个容器的元素,并将处理后的数据与基数按大小合并成一个数组,返回。

function quickSort(arr) {
// 递归出口就是数组长度为 1
if (arr.length <= 1) return arr;
//获取中间值的索引,使用 Math.floor 向下取整;
let index = Math.floor(arr.length / 2)
// 使用 splice 截取中间值,第一个参数为截取的索引,第二个参数为截取的长度;
// 如果此处使用 pivot=arr[index]; 那么将会出现无限递归的错误;
// splice 影响原数组
let pivot = arr.splice(index, 1)[0],
left = [],
right = [];
for (let i = 0; i < arr.length; i++) {
arr[i] < pivot ? left.push(arr[i]):right.push(arr[i]);
}
return quickSort(left).concat([pivot], quickSort(right));
}
// 第二种方法
function quickSort([first, ...rest]){
if(arguments[0].length <= 1) return arguments[0];
return [...quickSort(rest.filter(v => v < first)),
first,
...quickSort(rest.filter(v => v >= first))]
}
归并排序 O(nlog2n)
将两个有序数列合并成一个有序数列,我们称之为“归并”
基本思想与过程:先递归的分解数列,再合并数列(分治思想的典型应用)
思路
- 将一个数组拆成 A、B 两个小组,两个小组继续拆,直到每个小组只有一个元素为止。
- 按照拆分过程逐步合并小组,由于各小组初始只有一个元素,可以看做小组内部是有序的,合并小组可以被看做是合并两个有序数组的过程。
- 对左右两个小数列重复第二步,直至各区间只有 1 个数。
const merge = (left, right) => { // 合并数组
let result = []
// 使用 shift() 方法偷个懒,删除第一个元素,并且返回该值
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift())
} else {
result.push(right.shift())
}
}
result.push(...left, ...right)
return result
}
let mergeSort = function (arr) {
if (arr.length <= 1) return arr;
let mid = Math.floor(arr.length / 2)
// 拆分数组
let left = arr.slice(0, mid),
right = arr.slice(mid);
let mergeLeftArray = mergeSort(left),
mergeRightArray = mergeSort(right)
return merge(mergeLeftArray, mergeRightArray)
}
let arr = [2, 9, 6, 7, 4, 3, 1, 7, 0, -1, -2]
console.log(mergeSort(arr))
插入排序 O(n2)
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
思路
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置;
- 重复步骤 2~5。

let insertionSort = function (arr) {
for (let i = 1; i < arr.length; i++) {
let preIndex = i - 1,
cur = arr[i];
while (preIndex >= 0 && arr[preIndex] > cur) {
arr[preIndex + 1] = arr[preIndex]
preIndex--;
}
arr[preIndex + 1] = cur
}
return arr
}
let arr = [2, 9, 6, 7, 4, 3, 1, 7, 0, -1, -2]
console.log(insertionSort(arr))
选择排序 O(n2)
每一次从待排序的数组元素中选择最大(最小) 的一个元素作为已排序数组的尾元素,直到排完为止
思路
- 有 n 个数,需要排序 n-1 次
- 第一次选择最小值,放在第一位
- 第二次选择最小值,放在第二位
- …..重复该过程
- 第 n-1 次选择最小值,放在第 n-1 位

let selectSort = function (arr, flag = 0) {
let len = arr.length,
temp = 0;
// 一共需要排序 len-1 次
for (let i = 0; i < len - 1; i++) {
temp = i; // 最小的元素下标
// 从待排序的数组元素中选择最小元素的索引
for (let j = i + 1; j < len; j++) {
if (arr[j] < arr[temp]) {
temp = j;
}
}
// 每一趟保证第 i 位为最小值
if (temp !== i) {
[arr[i], arr[temp]] = [arr[temp], arr[i]]
}
}
return flag ? arr.reverse() : arr
}
let arr = [2, 9, 6, 7, 4, 3, 1, 7, 0, -1, -2]
console.log(selectSort(arr, 1))方便获取更多学习、工作、生活信息请关注本站微信公众号







 湘公网安备 43102202000103号
湘公网安备 43102202000103号